1. Масштаби
Масштабом називається відношення лінійних розмірів зображення,
поданого на кресленні, до відповідних розмірів предмета. Масштаби зображень
на кресленнях слід вибирати з такого ряду (ГОСТ 2.302-68):
масштаби зменшення—1:2; 1:2,5;
1:4; 1:5; 1:10; 1:15; 1:20; 1:25; 1:40; 1:50; 1:75; 1:100; 1:200; 1:400; 1:500;
1:800; 1:1000;
натуральна (справжня) величина
—1:1;
масштаби збільшення —2:1;
2,5:1; 4:1; 5:1; 10:1; 20:1; 40:1; 50:1; 100:1.
Перевагу слід надавати
зображенню предмета в натуральну величину.
Масштаб, указаний у призначеній
для цього графі основного напису креслення, позначається так: 1:1; 1:2; 4:1 і
т.д., а у всіх інших випадках — М1:1; М1:2; М4:1 і т.д.
2. Побудова похилу та конусності
Нахил однієї лінії
відносно іншої, розташованої переважно горизонтально або вертикально,
характеризує величину, яка називається похилом.
Для визначення похилу прямої
нахиленої до горизонтальної прямої l під кутом α (С — точка перетину цих прямих), беруть на
прямій t довільну точку А (рис. 4.21) і з неї опускають перпендикуляр на
пряму l. Відношення
АВ/ВС, виражене простим дробом або у відсотках, показує похил прямої t до
прямої l.
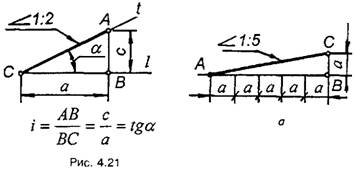 
Похил позначається на кресленні
знаком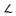 (див. рис. 4.21). Щоб побудувати заданий похил, наприклад 1:5, на горизонтальній
прямій відкладають п'ять рівних довільних відрізків а (рис. 4.22,а), які утворюють
відрізок АВ. Потім з кінця В ставлять перпендикуляр ВС
завдовжки а. Сполучивши точки С і А, отримують лінію, побудовану з
похилом 1:5. (див. рис. 4.21). Щоб побудувати заданий похил, наприклад 1:5, на горизонтальній
прямій відкладають п'ять рівних довільних відрізків а (рис. 4.22,а), які утворюють
відрізок АВ. Потім з кінця В ставлять перпендикуляр ВС
завдовжки а. Сполучивши точки С і А, отримують лінію, побудовану з
похилом 1:5.
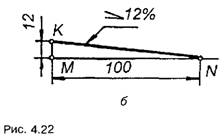
На рис. 4.22,б показано побудову
похилу 1:12. Будують горизонтальну пряму МN=100 од. З точки М ставлять
перпендикуляр до МN, на якому відкладають відрізок МК= 12 од.
Сполучивши точки К і N, отримують похил 1:12, або 12%.
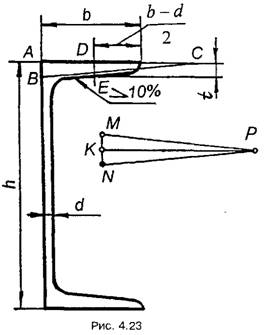 
Поверхні багатьох виробів мають
різні похили. Розглянемо креслення полички швелера (рис. 4.23). За розмірами
h, b, d, узятими зі стандарту, креслять основний контур швелера.
Визначаючи розмір (b-d)/2, знаходять точку D і відкладають від неї
величину t=DЕ. Через знайдену точку Е проводять пряму з похилом 1:10.
Це можна зробити двома способами:
1.
На основі полички швелера
відкладають відрізки AС=10 та АВ=1 і через точку E проводять пряму,
паралельну гіпотенузі ВС.
2.
На вільному місці
креслення проводять лінії МР та NР, які мають похил 1:10, і через точку
Е проводять пряму, паралельну NР.
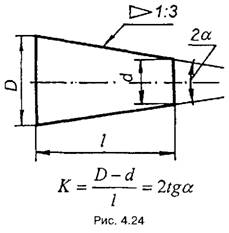
Конусність визначають як відношення різниці діаметрів двох
поперечних перерізів конуса до відстані між ними (рис. 4.24)
Конусність можна подати простим
дробом або у відсотках.
Конусність позначається на
кресленні знаком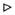 (див. рис. 3.23). (див. рис. 3.23).
3. Спряження ліній
Під час виконання креслень
предметів часто доводиться плавно сполучати між собою різні лінії.
Плавний перехід від
однієї лінії до іншої, виконаний за допомогою проміжної лінії, називається
спряженням.
Основні елементи спряження —
радіус спряження, центр спряження, точки спряження. При побудові спряжень
зазвичай задають радіус дуги спряження, а інші елементи визначають у процесі
побудови.
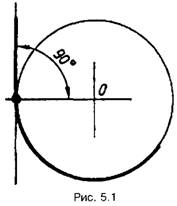
Плавний перехід між прямою і
дугою забезпечується лише тоді, коли пряма є дотичною до дуги, тобто точка
спряження розміщується на перпендикулярі, опущеному на пряму з центра кола
дуги спряження (рис. 5.1).
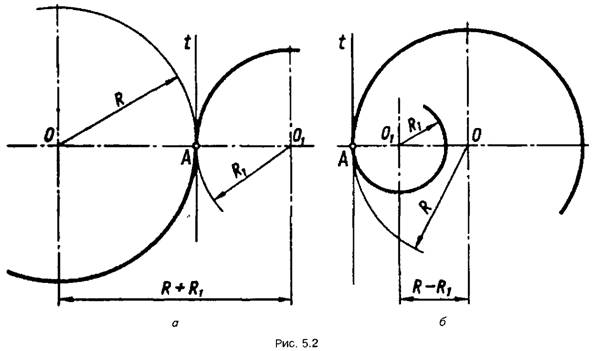
Плавний перехід між двома
колами (рис. 5.2) забезпечується в тому випадку, якщо обидва кола мають спільну
дотичну а точка спряження А лежить на прямій, що сполучає центри кіл.
Дотик називається зовні шнім, якщо центри О і О1, лежать з
різних боків від дотичної t (рис. 5.2,а), і внутрішнім, якщо центри розміщені
з одного боку від загальної дотичної (рис. 5.2,б). У разі зовнішнього дотику
відстань між центрами кіл дорівнює сумі їхніх радіусів (R+R1), а в
разі внутрішнього — різниці їхніх радіусів (R-R1).
3.1 Спряження прямих дугою кола
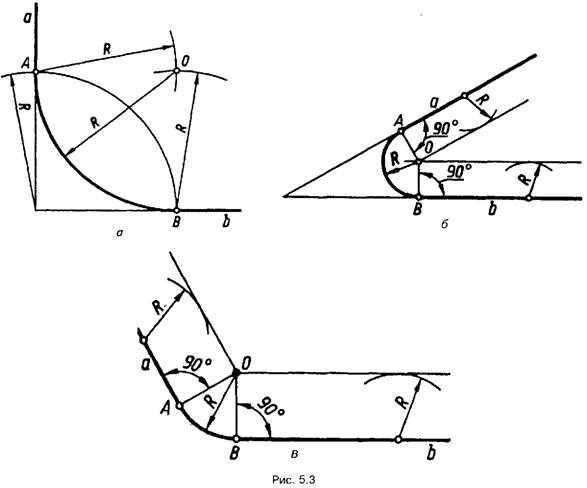
Розглянемо спряження сторін
прямого, гострого або тупого кутів (рис. 5.3,а-в) дугою радіуса R (заокруглення
кутів). Проводять дві допоміжні прямі, паралельні сторонам кута, на відстані
радіуса спряження R. Ці прямі є геометричним місцем центрів кіл радіуса R, дотичних до сторін кута. Точка О перетину цих прямих є
центром дуги спряження. Перпендикуляри, опущені з центра на задані прямі,
визначають точки спряження А і В. Радіусом R проводять дугу
спряження між точками А і В.
3.2 Спряження дуг між собою
Розрізняють три типи спряжень
дуг кола між собою: зовнішнє, внутрішнє і змішане.
Умови можливості розв'язання
задач на побудову спряжень двох кіл такі:
для зовнішнього спряження
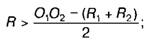
для внутрішнього спряження
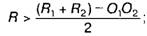
для змішаного спряження
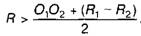
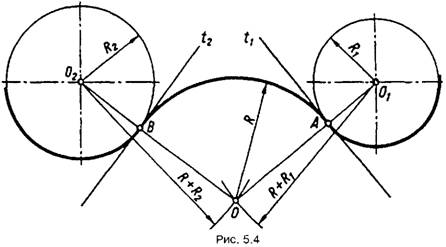 
На рис. 5.4 показане зовнішнє спряження
радіусом R двох кіл радіусів
R1 і R2. Центр спряження О лежить у точці перетину двох
допоміжних дуг радіусів R +R1 і R +R2, проведених
відповідно з центрів О1 і O2.
Точки спряження А і В
визначають як точки перетину заданих дуг з прямими O1O і O2O.
Призовнішньому спряженні спряжувані дуги розташовані з зовнішнього боку дуги
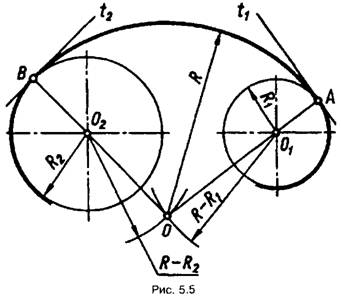
спряження із різних боків дотичних t1 і t2.Внутрішнє
спряження показане на рис.5.5. Внутрішнє спряження двох дуг третьою дугою
характеризується тим, що спряжувані дуги розташовані всередині дуги спряження,
тобто дуга спряження і спряжувані дуги лежать з одного боку дотичних і
проведених через точки спряження. З центрів О1 і O2
проводять дві допоміжні дуги радіусів R - R1 і R - R2. На
перетині цих дуг отримуємо центр спряження О. Прямі O1O і O2O,
перетинаючи задані дуги, дають точки спряження А і В.
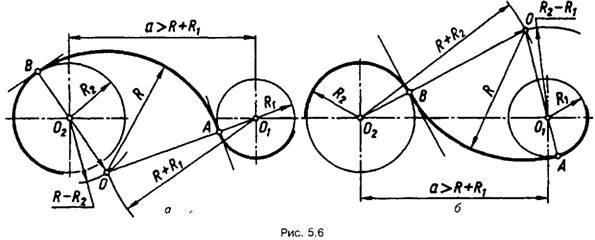
Змішане спряження (рис. 5.6)
характеризується тим, що одна спряжувана дуга розміщена всередині дуги
спряження, а друга — поза нею.
На рис. 5.6,а дуга спряження
має з дугою радіуса R2 внутрішнє спряження, а з дугою радіуса R1
— зовнішнє. З центра O2 проведемо дугу радіусом R - R2, а
з центра O1 радіусом R+R1. Перетин цих дуг є центром дуги
спряження. Точки спряження А і В лежать на перетині кіл з
прямими ОО1 та OO2.
На рис. 5.6,б показане змішане
спряження цих же дуг, однак при цьому дуга спряження має з дугою радіуса R2
зовнішнє спряження, а з дугою радіуса R1 — внутрішнє. Побудова аналогічна
побудові на рис. 5.6,а.
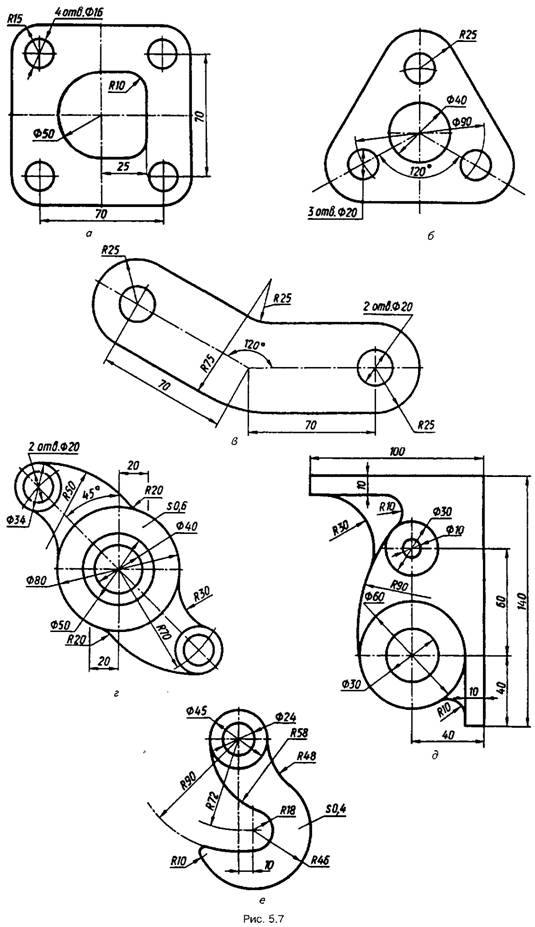
На рис. 5.7 подано креслення
деталей, у яких виконані описані вище спряження: на рис. 5.7,а —
спряження сторін прямого кута; на рис. 5,7,б — спряження сторін гострого кута;
на рис. 5.7,в — спряження сторін тупого кута; на рис. 5.7,г— зовнішнє
спряження; на рис. 5.7, д — внутрішнє спряження; на рис. 5.7,е — змішане
спряження.
| 
